GRAPHES (THÉORIE DES)

GRAPHES (THÉORIE DES)

On appelle théorie des graphes une classe de problèmes plus ou moins bien résolus. Leur résolution suscite chez les mathématiciens, en particulier à l’étranger, un engouement sans cesse croissant.

Claude Berge, dans le discours inaugural des Journées internationales d’études de la théorie des graphes (1966), déclare: «Je remercie les deux cent cinquante participants de ce congrès venus si nombreux à Rome pour un sujet qui, il y a dix ans seulement, n’aurait attiré qu’une dizaine de personnes. Étrange évolution que celle de la théorie des graphes, qui se développe par à-coups, sous l’impulsion tour à tour du rôle de l’électricité, de la géométrie des polyèdres, de la théorie des jeux, et surtout maintenant de la recherche opérationnelle et du calcul électronique.»

Depuis 1966, on a pu en effet remarquer que les Mathematical Reviews , périodique qui recense et résume la plupart des articles de mathématiques parus, ont ouvert une rubrique intitulée «Théorie des graphes». Située dans cette publication entre la théorie des ensembles et la logique mathématique, elle rend compte d’articles toujours plus nombreux.

La théorie des graphes est relativement récente. L’originalité de son champ propre du point de vue psychologique est surprenante: elle tient, nous semble-t-il, à ce que des problèmes et des concepts particulièrement compliqués, arbitraires et rébarbatifs dans leur écriture formelle peuvent être aisément compris. Il suffit pour cela de consentir à ce que des «petits dessins» – auxquels les théoriciens des graphes ont systématiquement recours – fécondent l’intuition.

Nous présenterons d’abord quelques grands problèmes de la théorie des graphes, dont l’exposé formel concis serait incompréhensible. Nous signalerons, pour finir, un domaine de la théorie pour lequel l’algébrisation des concepts a atteint une grande rigueur, rigueur qui reste à tout instant justifiée par l’efficacité des notions introduites.

Définitions

Les nombreuses définitions des graphes caractérisent en fait des êtres voisins. Ces définitions ne sont pas toujours du même type algébrique. Tel auteur dira que les graphes qu’il considère sont essentiellement finis, tel autre réservera le nom de graphes aux graphes non orientés, tel autre encore dira qu’un graphe est une correspondance d’un ensemble fini dans lui-même...

Cet article se limitera aux multigraphes orientés ou non, en omettant – comme de nombreux auteurs – le préfixe multi, et en permettant les boucles.

Graphes orientés

Plus précisément, on appellera graphe orienté un quadruplet (X, face=F9796 U, o , e ), où X désigne un ensemble appelé ensemble des sommets du graphe; face=F9796 U un ensemble appelé ensemble des arcs du graphe; o une application de face=F9796 U dans X appelée origine; e une application de face=F9796 U dans X appelée extrémité.

Cette définition, pour rigoureuse qu’elle soit du point de vue algébrique, n’est certes pas un support très engageant pour l’intuition. Et pourtant, si l’on accepte de représenter les éléments de X par des points du plan, et tout élément de face=F9796 U par une «flèche» partant du point représentatif de son image par o pour aboutir au point représentatif de son image par e , on obtient de petits dessins du genre de ceux de la figure 1.

De tels dessins évoquent des problèmes réels tels qu’il s’en pose en sociologie, en recherche opérationnelle, en physique, etc.; peu de disciplines scientifiques y échappent.

Une telle représentation d’un graphe par des points et des arcs de Jordan simples est appelée représentation géométrique du graphe, ou simplement graphe géométrique .

Graphes non orientés

Les flèches ne sont pas indispensables à nos petits dessins. Un graphe sans flèche, classiquement appelé non orienté , peut être donné par un ensemble X de sommets et un ensemble A de couples non ordonnés d’éléments de X, appelés arêtes . Les représentations géométriques de tels graphes ne posent aucun problème particulier (fig. 2).

Théorèmes de Kuratowski et Youngs-Ringel

Commençons par un problème de topologie du plan que la théorie des graphes a transformé en problème combinatoire.

Un jeu connu des journaux enfantins consiste à tenter de faire tracer des chemins partant de trois maisons et allant vers trois puits... sans que ces chemins se coupent (fig. 3). Le problème est sans solution. On dit que le graphe K^3,3 n’est pas planaire. Plus généralement, un graphe est planaire s’il en existe une représentation géométrique dans laquelle les arcs ne se coupent pas.

Le Polonais Kuratowski (1930) a montré que ni K^3,3 ni K⁵ ne sont planaires (fig. 4) et a trouvé une étonnante caractérisation des graphes planaires. Posons deux définitions préliminaires. On dit qu’un graphe G contient un graphe G si l’on peut obtenir G à partir de G en effaçant des sommets et des arêtes de G. On dit que l’on peut contracter G en un graphe G , si, en supprimant tous les sommets auxquels n’arrivent que deux arêtes de G et en les remplaçant par des arêtes, on obtient G (fig. 5).

Savoir si un graphe est planaire, c’est savoir s’il en existe une représentation géométrique dans le plan (ou sur une surface quelconque de genre 0) telle que les représentations des arêtes ne se coupent pas; la planarité est donc une question de géométrie différentielle puisqu’il s’agit de tracer des courbes continues sur des surfaces. Et cependant, le théorème de Kuratowski affirme qu’un graphe G est planaire si, et seulement si, il ne contient aucun graphe G qui puisse être par contraction rendu identique à K^3,3, ou à K⁵, ce qui est une caractérisation purement combinatoire.

La question de la planarité, ou plus généralement de la représentation géométrique des graphes sur des variétés (surfaces), est une question fondamentale.

Dans chaque congrès de théorie des graphes, plusieurs fois par an, de très nombreux problèmes sont proposés, tandis que l’on résout enfin des problèmes non résolus depuis des époques relativement lointaines. C’est ce qui est arrivé en 1968 à la conjecture de P. J. Heawood .

On a vu que K⁵, encore appelé graphe complet à cinq sommets, n’est pas planaire, c’est-à-dire n’admet pas de «bonne représentation» sur le plan, en appelant «bonne représentation» une représentation géométrique dans laquelle les images des arêtes ne se couperaient pas. On voit facilement que sur un tore et plus généralement sur une surface de genre au moins égal à 1 (c’est-à-dire comme le tore «percé d’au moins un trou»; cf. FONCTIONS ANALYTIQUES - représentation conforme; TOPOLOGIE - Topologie algébrique), K⁵ admet une bonne représentation (fig. 6). D’une façon plus générale, appelons Kⁿ le graphe à n sommets dans lequel tout couple de sommets différents est une arête. Appelons genre d’un graphe G le minimum du genre des variétés sur lesquelles on peut trouver une bonne représentation géométrique de G.

La conjecture posée par P. J. Heawood à la fin du XIX^e siècle consiste à dire que le genre de Kⁿ est égal au plus petit entier immédiatement supérieur à:

Cette conjecture a été démontrée d’année en année pour chaque cas particulier de n modulo 12 en commençant par les plus simples, mais elle n’a été résolue complètement qu’en 1969 par T. Youngs et G. Ringel. Il faut un petit livre pour en faire la démonstration complète, et, si le résultat n’est guère sophistiqué dans son énoncé, la méthode de démonstration fait souvent appel à des secteurs très formalisés des mathématiques.

Problèmes d’Euler et de Hamilton

«Des problèmes où l’on se fait tout petit pour se promener le long des arêtes d’un graphe.»

Le problème d’Euler

Ce problème classique de cheminement le long des ponts de Königsberg, ville de l’ancienne Prusse-Orientale, souleva l’intérêt du célèbre mathématicien suisse Leonhard Euler. On parlait alors beaucoup du problème des ponts. Le plan de la ville (aujourd’hui Kaliningrad, en U.R.S.S.) peut être schématisé comme sur la figure 7 et le problème posé par les oisifs prussiens était: peut-on se promener dans Königsberg en passant une fois et une seule par chaque pont et en revenant à son point de départ?

Ce problème devient un problème de graphes dans la représentation de la figure 7. Il faut alors trouver un chemin qui passe par toutes les arêtes une fois et une seule et qui revienne à son point de départ. Un tel chemin est appelé de nos jours un cycle eulérien , notion qui se formalise aisément.

Euler démontra que ce problème était insoluble et que, plus généralement, pour qu’il existe dans un graphe G un cycle eulérien, il faut et il suffit que, pour tout sommet de G, le nombre d’arêtes qui aboutissent à ce sommet soit pair.

Le problème de Hamilton

À côté de ce problème bien résolu de cheminement, il est un problème proposé par W. R. Hamilton en 1859, et qui est de mieux en mieux étudié, mais toujours très imparfaitement.

On appelle chemin hamiltonien dans un graphe orienté une succession de sommets et d’arcs telle que tous les sommets apparaissent une fois et une seule dans la succession et telle que deux sommets successifs x ⁱ , x ⁱ⁺¹ sont séparés par un arc u ⁱ d’origine x ⁱ et d’extrémité x ⁱ⁺¹ . On appelle circuit hamiltonien un chemin hamiltonien tel qu’il existe un arc allant du dernier sommet au premier sommet de la succession.

Le problème est de trouver une condition nécessaire et suffisante pour qu’un graphe G contienne un circuit hamiltonien. De très nombreuses conditions nécessaires ont été trouvées, ainsi que de nombreuses conditions suffisantes, mais aucune bonne condition nécessaire et suffisante n’est apparue jusqu’à ce jour. Les démonstrations des théorèmes correspondants sont parfois très difficiles, souvent inattendues. Citons deux exemples, l’un relativement ancien, l’autre récent.

On appelle tournoi un graphe orienté de n sommets tel que, pour tout couple (x , y ), de sommets distincts, il existe un arc de graphe soit d’origine x et d’extrémité y , soit d’origine y et d’extrémité x (fig. 8).

Théorème de L. Redei . Dans un tournoi, il existe un chemin hamiltonien.

Imaginons qu’un arc d’origine x et d’extrémité y signifie «qu’au cours d’un tournoi x l’a emporté sur y ». On voit qu’à l’«issue du tournoi» il existe au moins une façon de ranger les joueurs qui soit un ordre total. Alors que ce théorème peut se démontrer avec des moyens simples et un fort support intuitif, il faut une formalisation très raffinée pour démontrer le suivant.

Théorème de A. Gouihla-Houri. . Si G est un graphe orienté sans boucles à n sommets tel que pour tout sommet x de G le nombre des arcs ayant pour origine ou extrémité x soit strictement supérieur à n , alors G contient un circuit hamiltonien.

Coloriage

Quand on commence par jouer avec des crayons de couleur, on finit par faire de l’algèbre de bords et de cobords.

Les théoriciens des graphes, amateurs de petits dessins, ne pouvaient manquer de chercher à y mettre des couleurs! Mais sous ces structures multicolores se cachaient des structures algébriques que l’on met progressivement au jour... et elles résistent avec beaucoup d’énergie. Le problème des quatre couleurs , qu’a bien situé un article du mathématicien anglais A. Cayley, paru en 1879 dans le volume I des comptes rendus de la Société royale de géographie, est de ceux que Franck Harary appelle graphical disease .

Il s’agit de démontrer une propriété des cartes de géographie bien connue empiriquement des topographes. Posons intuitivement le problème au moyen d’une carte arbitraire des départements d’un pays imaginaire. On a pu démontrer que si les arêtes de la représentation géométrique de cette carte étaient des arcs de Jordan simples, alors cinq crayons de couleurs différentes suffisaient pour colorier les départements de telle façon que deux départements ayant une frontière commune non réduite à un point aient toujours des couleurs différentes.

Expérimentalement, on a constaté que toute carte pouvait être coloriée avec quatre couleurs au plus. C’est l’origine d’une célèbre conjecture en mathématiques, le problème des quatre couleurs , qui a suscité une littérature considérable. Plusieurs ouvrages sont exclusivement consacrés aux conséquences qui en découlent. Ce problème entre dans le cadre de la théorie des graphes au moyen de la transformation indiquée sur la figure 9. À chaque département on fait correspondre un sommet du graphe et l’on trace une arête entre deux sommets toutes les fois que les départements correspondants ont une frontière commune non réduite à un point. Trouver un coloriage de cette carte en quatre couleurs revient à trouver une application C de l’ensemble des sommets dans1, 2, 3, 4 telle que deux sommets liés par une arête n’aient jamais la même image.

Quant à la propriété caractéristique des graphes associés aux cartes de géographie, nous la connaissons déjà: ce sont tous des graphes planaires. On voit donc que, grâce au théorème de Kuratowski, on peut formaliser le problème du coloriage en termes purement combinatoires.

Ce problème célèbre des quatre couleurs a été résolu affirmativement par K. Appel et W. Haken en 1976. Leur démonstration, vu le nombre très grand de configurations réductibles à tester, nécessite un temps important d’ordinateur. C’est le premier exemple de théorème général obtenu par cette voie. Une telle démonstration pose un problème épistémologique: vu l’importance des moyens informatiques utilisés, sa vérification est difficilement reproductible (cf. J. Mayer, «Solution du problème des quatre couleurs», in Universalia 1978 , Encyclopaedia Universalis éd., Paris, 1978).

Flots et tensions

Voici un problème bien formalisé, et pour lequel la formalisation est utile.

Le problème des affectations, des transports, des flots et des tensions révèle sous ses différents noms les multiples facettes d’une même réalité algébrique. Il se pose et s’est posé historiquement dans des cadres pratiques apparemment très différents. Empruntons deux exemples caractéristiques à Claude Berge.

Affectation optimale du personnel (D. Votaw et A. Orden). Considérons p ouvriers a ¹, a ², ..., a ^p que l’on veut répartir sur q machines a ¹, ..., a ^q . Le rendement de l’ouvrier sur la machine a ¹ est donné par un nombre k ^{i j} . Comment affecter les ouvriers pour maximiser le rendement total?

Problème des trajets maritimes à vide (B. O. Koopmans). Considérons le trafic des cargos en 1913: certains ports, comme Lisbonne, San Francisco, Athènes, Yokohama, exportent peu et importent beaucoup; d’autres ports, tels New York, La Plata, Odessa, Rotterdam, exportent beaucoup et importent peu. Il faudra donc envoyer les cargos à vide le long des lignes maritimes usuelles, de façon à satisfaire les demandes en navires vides de New York, La Plata, etc. Connaissant la longueur l ⁱ de la traversée sur la ligne maritime i , on veut minimiser le coût de ce rapatriement.

La formalisation mathématique de ces problèmes nécessite une série de définitions.

On appelle graphe de transport un graphe orienté où l’on distingue deux sommets, la sortie et l’entrée, et un arc qui les relie (fig. 10). Dans un tel graphe, à tout couple de sommets quelconques (x ⁱ , x ^j ) liés par un arc, on affecte deux nombres b ^ij et c ^ij (b^ij 諒 c ^ij ) appelés capacités de l’arc.

Supposons que les arcs désignent des chemins à sens unique le long desquels on fait circuler des personnes en nombre supérieur à b ^ij et inférieur à c ^ij . Si la capacité supérieure de l’arc qui relie l’entrée et la sortie est infinie et sa capacité inférieure nulle, on se propose de trouver les débits entiers des différents arcs, tels que le débit de l’arc s soit maximal (resp. min.).

Un ensemble de débits satisfaisant à cette question est appelé un flot maximal (resp. min.). On peut munir l’ensemble de ces problèmes de structures algébriques linéaires sur lesquelles on sait raisonner. À chaque flot on associe un vecteur d’un certain module (cf. algèbre LINÉAIRE ET MULTILINÉAIRE) des flots qui est orthogonal à un certain autre module des tensions.

Numérotons les arêtes du graphe de 1 à n . À chaque flot on peut associer un n -uple dont les éléments sont les n débits du flot. Ces n -uples peuvent être considérés comme des éléments d’un module de type fini.

Si l’on associe à chaque sommet du graphe un entier quelconque, on dit que l’on a muni le graphe d’un potentiel . Ce potentiel induit sur les arcs du graphe un ensemble de tensions. Les tensions forment un module orthogonal à celui des flots.

Une chaîne d’un graphe est une suite de sommets et d’arcs commençant et finissant par un sommet et telle qu’entre deux sommets consécutifs il y ait un arc allant du premier vers le second ou du second vers le premier. Un cycle est un ensemble de chaînes fermées. Un cocycle est un ensemble d’arcs dont une extrémité est dans un sous-ensemble A de X et l’autre dans le complémentaire de A.

Les modules des flots et tensions ont eux-mêmes des conditions d’orthogonalité intéressantes avec les vecteurs-cycles et les vecteurs-cocycles. Ces «vecteurs» interprètent dans les termes du calcul linéaire les propriétés des cycles et des cocycles. Les propriétés des modules permettent alors de démontrer l’existence des flots d’une façon particulièrement élégante. Deux définitions supplémentaires sont indispensables à l’expression d’une telle condition nécessaire et suffisante d’existence.

Si 諸^A désigne le cocycle de A, on note 諸^A+ l’ensemble des arcs du cocycle qui ont leur origine dans A, et 諸^A- l’ensemble des arcs du cocycle qui ont leur origine dans le complémentaire de A.

Un cocycle est élémentaire si A et son complémentaire sont non vides. Dans ces conditions, pour tout x contenu dans A, et y n’appartenant pas à A, il existe une chaîne passant par x et y . On peut maintenant énoncer le théorème d’Hoffmann : étant donné des nombres b ^ij et c ^ij , avec b ^ij 諒 c ^ij (i , j étant les indices des sommets du graphe liés par un arc), la condition nécessaire et suffisante pour qu’il existe un flot 﨏 tel que b ^ij 諒 﨏^ij 諒 c ^ij , 﨏^ij désignant le flot qui parcourt l’arc ij , est que, pour tout cocycle élémentaire 諸, on ait: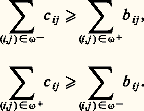

À ce genre de problème, la formalisation apporte, en plus de la solution, le sentiment d’«y voir clair», de comprendre les structures des «phénomènes mathématiques» qui leur sont associés!

Qu’apporte en retour la théorie des graphes aux mathématiques formelles? Sans contredit une mine de problèmes nouveaux dans lesquels l’intuition peut être très efficace, et ce d’autant plus qu’elle est puissamment soutenue par de petits dessins! En raison peut-être du rôle que joue l’intuition dans son développement, en raison de la nouveauté des problèmes auxquels elle s’attaque, en raison enfin de la proximité des applications, la théorie des graphes a longtemps été à l’étranger et demeure en France l’objet d’une certaine suspicion de la part des mathématiciens traditionnels. Il reste à espérer que la mathématique en train de se faire pourra recevoir de la mathématique en train de se parfaire hommage et lettres de noblesse.

Encyclopédie Universelle. 2012.